Francisco Yepes Barrera
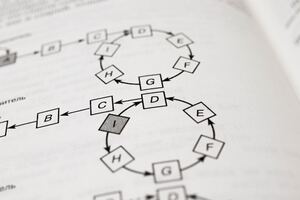
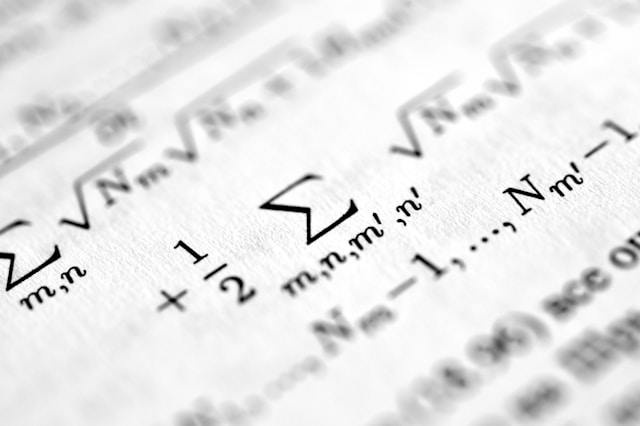Backpropagation is a generalization of the Delta rule to be able to take into account non-linear functions....
Month: August 2020
Euclid defined the golden section or golden ratio in the following way: Split a segment into two...
The Schrödinger equation $$-\frac{\hbar}{i}\frac{\partial\Psi(x,t)}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^{2}\Psi(x,t)}{\partial x^{2}}+V(x,t)\Psi(x,t)$$ involves a state function (\(\Psi\) wave function) which depends on spatial...
Degeneration occurs when two or more independent wave functions have the same eigenvalue. It is said that...
