Conservation of Angular Momentum in a System of Central Forces

In physics, both classical mechanics and quantum mechanics, we define angular momentum as the cross product of the radius and the linear momentum:

$$\mathbf{L}=\mathbf{r}\times m\mathbf{v}$$

with $\mathbf{L}$ a vector perpendicular to $\mathbf{r}$ and $\mathbf{v}$ according to the right-hand rule.

From the definition of cross product, the modulus of $\mathbf{L}$ is given by:

$$\left\Vert \mathbf{L}\right\Vert =\left\Vert \mathbf{r}\right\Vert \left\Vert \mathbf{v}\right\Vert \sin\theta$$

with $\theta$ the angle between the vectors $\mathbf{r}$ and $\mathbf{v}$.

Torque is the temporal variation of angular momentum, symbolized by the letter $\tau$:

$$\mathbf{\tau}=\frac{d\mathbf{L}}{dt}$$

Torque is also known as moment of force, and is the rotational analog of linear force. In a system of central forces, it is zero. Let’s see why.

Taking into account the mathematical properties of the cross product, considering that $\frac{d\mathbf{r}}{dt}=\mathbf{v}$, and that the cross product of a vector with itself is zero, we have :

$$\frac{d\mathbf{L}}{dt}=m\frac{d}{dt}\left(\mathbf{r}\times\mathbf{v}\right)=m\left(\frac{d\mathbf{r}}{dt}\times\mathbf{v}+\mathbf{r}\times\frac{d\mathbf{v}}{dt}\right)=m\left(\mathbf{r}\times\frac{d\mathbf{v}}{dt}\right)=\mathbf{r}\times\frac{d}{dt}(m\mathbf{v})=\mathbf{r}\times\mathbf{F}$$

The time variation of angular momentum is equal to the cross product of the radius and the time variation of the linear momentum, i.e., the force. The modulus of this vector is:

$$\left\Vert \frac{d\mathbf{L}}{dt}\right\Vert =\left\Vert \mathbf{r}\right\Vert \left\Vert \mathbf{F}\right\Vert \sin\theta$$

But the force, as well as the acceleration and radius, is directed towards the center. Therefore, radius and force form an angle of zero degrees, so:

$$\frac{d\mathbf{L}}{dt}=0$$

and $\mathbf{L}$ is constant.

Let us now consider the following figure:

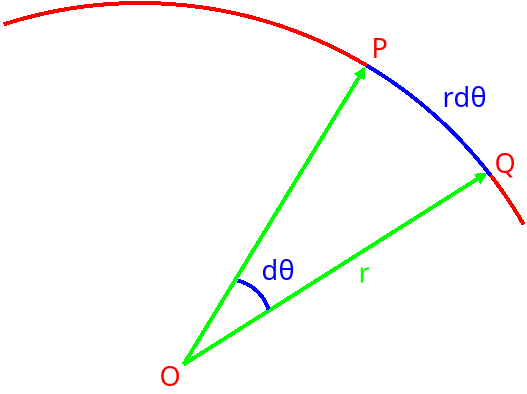
The circumference fraction given by $d\theta$ is $\frac{d\theta}{2\pi}$. The length of the circular segment is, therefore:

$$2\pi r\frac{d\theta}{2\pi}=rd\theta$$

We can write the differential element of area $dA$ (triangle $OPQ$) as the absolute value of the following cross product (half the product base $\times$ height):

$$dA=\frac{1}{2}\left|\mathbf{r}\times\mathbf{r}d\theta\right|$$

The temporal variation of this differential area element is linked to the temporal variation of the angle, which in turn is linked to the velocity $\mathbf{v}$:

$$\frac{dA}{dt}=\frac{1}{2}\left|\mathbf{r}\times\mathbf{r}\frac{d\theta}{dt}\right|=\frac{1}{2}\left|\mathbf{r}\times\mathbf{v}\right|$$

Since $\mathbf{L}=m(\mathbf{r}\times \mathbf{v})$ is constant in a system of central forces, the time variation of the area is also constant.

Suppose a planet orbits the sun following an elliptical curve that approaches the perihelion of the orbit. The planet increases its speed, which becomes maximum at the perihelion point, while the radius decreases. A symmetric consideration can be done in the approximation of the planet to the aphelion of the orbit. The relationship between these two quantities is such that the cross product (the area covered between two instants of time) is constant. In practice, Kepler’s second law: