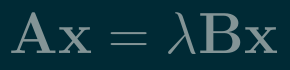
Table of Contents
Problem Definition
The eigenvalue problem is an essential component of many numerical methods, especially in science and technology. Mathematically, it is defined as
\begin{equation}\mathbf{A}\mathbf{x}=\lambda\mathbf{x}\end{equation}where \mathbf{A} is a square matrix, \lambda represents the eigenvalues, and \mathbf{x} the eigenvectors. For a square matrix \mathbf{A} (n\times n), the resolution of this system leads to n eigenvalues (real or complex) and n eigenvectors, each with n components.
When considering a linear transformation represented by a matrix \mathbf{A}, the eigenvectors are special vectors that, under the action of \mathbf{A}, are only lengthened or shortened but not rotated or changed direction. The associated eigenvalue indicates the scale factor of this lengthening or shortening.
Therefore, the coordinate system formed by the eigenvectors differs from the original one only by the length of the vectors (multiplied by the corresponding eigenvalue). This property allows the matrix to be “diagonalized” or “simplified,” making it easier to analyze the behavior of the transformation along these special directions.
This type of problem is fundamental in mathematics and physics because it allows us to study the intrinsic properties of linear systems, such as the vibrational modes of a body, quantum states, system stability, and much more. However, calculating eigenvalues numerically can be delicate and sensitive to small variations in the data (problem conditioning), especially for non-symmetric matrices. For symmetric matrices, the problem is well-conditioned and more stable.
Equation (1) expresses in matrix form a system of equations:
\begin{pmatrix}
a_{11} - \lambda & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} - \lambda & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} - \lambda
\end{pmatrix}
\begin{pmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{pmatrix}
=
\begin{pmatrix}
0 \\
0 \\
\vdots \\
0
\end{pmatrix}or, in algebraic form
\begin{cases}
(a_{11} - \lambda) x_1 + a_{12} x_2 + \cdots + a_{1n} x_n = 0 \\
a_{21} x_1 + (a_{22} - \lambda) x_2 + \cdots + a_{2n} x_n = 0 \\
\vdots \\
a_{n1} x_1 + a_{n2} x_2 + \cdots + (a_{nn} - \lambda) x_n = 0
\end{cases}A particularly important version of the eigenvalue problem is the case where \mathbf{A} is real and symmetric. In the following discussion, we will consider only this type of matrix.
The problem can be rewritten using the identity matrix, \mathbf{I}:
\mathbf{A}\mathbf{x}=\lambda\mathbf{I}\mathbf{x}If we replace \mathbf{I} with a positive-definite matrix \mathbf{B} (n\times n), we obtain the generalized eigenvalue problem
\begin{equation}\mathbf{A}\mathbf{x}=\lambda\mathbf{B}\mathbf{x}\end{equation}The eigenvalues and eigenvectors of the generalized symmetric-definite eigenproblem are always real, and eigenvectors can be chosen to be orthogonal.
This problem reduces to the standard symmetric eigenvalue problem (1) by applying the Cholesky decomposition to \mathbf{B}:
\begin{array}{rcl}
\mathbf{A}\mathbf{x} & = & \lambda\mathbf{B}\mathbf{x}\\
\mathbf{A}\mathbf{x} & = & \lambda\mathbf{L}\mathbf{L}^{\intercal}\mathbf{x}\\
\left(\mathbf{L}^{-1}\mathbf{A}\mathbf{L}^{-\intercal}\right)\mathbf{L}^{\intercal}\mathbf{x} & = & \lambda\mathbf{L}^{\intercal}\mathbf{x}
\end{array}Therefore, the problem becomes \mathbf{C}\mathbf{y}=\lambda\mathbf{y} where \mathbf{C}=\mathbf{L}^{-1}\mathbf{A}\mathbf{L}^{-\intercal} is symmetric, and \mathbf{y}=\mathbf{L}^{\intercal}\mathbf{x}. The standard symmetric eigensolver can be applied to the matrix \mathbf{C}.
GNU Scientific Library (GSL)
The GNU Scientific Library (GSL) is a software library for numerical computations in applied mathematics and science. It is written in C and distributed under the GNU General Public License, making it free software. The library was created to offer a modern alternative to traditional Fortran libraries and is designed to be easily integrated into other programming languages via wrappers.
The GSL project was started in 1996 by Mark Galassi and James Theiler of Los Alamos National Laboratory with the aim of replacing older libraries. Subsequently, other developers, such as Brian Gough and Gerard Jungman, contributed substantially to the project. Version 1.0 was released in 2001, while development resumed with version 2.0 in 2015.
GSL offers a wide range of features for scientific computing, including:
| Complex Numbers | Quasi-Random Sequences | Discrete Hankel Transforms |
| Roots of Polynomials | Random Distributions | Root-Finding |
| Special Functions | Statistics | Minimization |
| Vectors and Matrices | Histograms | Least-Squares Fitting |
| Permutations | N-Tuples | Physical Constants |
| Sorting | Monte Carlo Integration | IEEE Floating-Point |
| BLAS Support | Simulated Annealing | Discrete Wavelet Transforms |
| Linear Algebra | Differential Equations | Basis splines |
| Eigensystems | Interpolation | Running Statistics |
| Fast Fourier Transforms | Numerical Differentiation | Sparse Matrices and Linear Algebra |
| Quadrature | Chebyshev Approximation | |
| Random Numbers | Series Acceleration |
Since it’s written in C, GSL is also easily usable in C++ and can be extended via wrappers to many other programming languages, such as Python, Java, Julia, R, Ruby, Rust, Fortran, and others.
GSL is widely used in academia and fields requiring reliable scientific calculations, offering stability, a wide range of features, and an active community for contributions and support. It’s suitable for anyone working with numerical calculations in C or in environments that integrate with C.
The official documentation can be found at the following link: https://www.gnu.org/software/gsl/doc/html/index.html.
LAPACK/LAPACKE
LAPACK (Linear Algebra PACKage) is a standard software library for numerical linear algebra, written in Fortran 90. It specializes in providing efficient and robust routines for solving common linear algebra problems, including:
| Simultaneous systems of linear equations | Eigenvalue and Singular Value Problems (SVD) |
| Linear least squares solutions | Matrix factorizations such as LU, QR, Cholesky, and Schur |
LAPACK was designed to take full advantage of modern machine architecture with cache memory and instruction-level parallelism, significantly improving performance compared to previous libraries such as LINPACK and EISPACK. Its success also depends on the extensive use of BLAS (Basic Linear Algebra Subprograms), a low-level library specializing in fundamental linear algebra operations, highly optimized for various hardware platforms. Version 1.0 was released on February 29, 1992. It is distributed under a modified BSD license, which is a free and permissive license.
LAPACK handles dense and banded matrices, both real and complex, in single or double precision, but does not handle general sparse matrices.
LAPACKE is the C version of LAPACK, an interface and library that allows using LAPACK functionality originally written in Fortran but accessible directly from C code. LAPACKE provides numerical linear algebra routines similar to those of LAPACK, with a more natural interface for C programmers.
Here are some key points about LAPACKE:
- LAPACKE is a high-level interface written in C that invokes the underlying LAPACK functions, written in Fortran.
- It allows calling routines for matrix computation, linear system resolution, factorization, and eigenvalue calculation directly from C programs without having to write Fortran code.
- It provides functions with more idiomatic names and parameters for C, making it easier to integrate into C/C++ applications.
- LAPACKE still relies on an efficient BLAS library, such as LAPACK, for optimal performance.
- It is particularly useful in contexts where the main code is in C or C++, but we want to take advantage of LAPACK’s performance and numerical routines without having to write or integrate Fortran code.
LAPACKE is the standard way to use LAPACK from C/C++ languages, making it easy to use LAPACK’s powerful linear algebra routines in more modern and widely used programming environments.
An Example: Secular System in Quantum Mechanics
In wave mechanics, the Schrödinger equation is given by
\hat{H}\psi=E\psiIt is an eigenvalue equation, where \hat{H} represents the Hamiltonian (energy) operator, \psi is the wave function, and E is the energy of the system.
This equation is solvable analytically only for some special cases, such as systems with a single electron (hydrogen-like). When there is more than one electron, an interelectron repulsion term appears in the Hamiltonian, leading to a non-separable differential equation.
In these cases, a trial function is used, that is, an approximate function composed of a linear combination of basis functions, \varphi_i, linearly independent functions of parameters, and weighted by coefficients c_i:
\begin{equation}\psi=\sum_{i=1}^{n}c_i \varphi_i\end{equation}The basis functions are often proper functions of analytically solvable systems, such as the states of the hydrogen atom, or Gaussian functions (called GTOs, Gaussian Type Orbitals).
The validity of this approximate approach lies in a result called the variational theorem, which states that any trial function will lead to an energy, E, greater than or equal to the true energy of the system, E_0:
\begin{equation}\left\{ E=\frac{\int\psi{}^{*}\hat{H}\psi\,d\mathbf{x}}{\int\psi{}^{*}\psi\,d\mathbf{x}}\right\} \geq E_0\end{equation}Mathematically, therefore, the energy calculation is configured as a minimum procedure in which the parameters of the functions \varphi_i are varied to lower E as much as possible and get closer to E_0.
Substituting equation (3) into (4) allows us to develop a procedure called the Rayleigh-Ritz variational method. This leads to the following system of equations, known as the secular system:
\sum_{k=1}^{n}\left[\left(H_{ik}-ES_{ik}\right)c_{k}\right]=0\begin{cases}
(H_{11} - E S_{11}) c_1 + (H_{12} - E S_{12}) c_2 + \cdots + (H_{1n} - E S_{1n}) c_n = 0 \\
(H_{21} - E S_{21}) c_1 + (H_{22} - E S_{22}) c_2 + \cdots + (H_{2n} - E S_{2n}) c_n = 0 \\
\quad \vdots \\
(H_{n1} - E S_{n1}) c_1 + (H_{n2} - E S_{n2}) c_2 + \cdots + (H_{nn} - E S_{nn}) c_n = 0
\end{cases}or, in matrix form
\begin{equation}\left(\mathbf{H}-E\mathbf{S}\right)\mathbf{c}=0\end{equation}which is equation (2) rearranged, a generalized eigenvalue problem, where E are the eigenvalues (energies of the system), \mathbf{c} are the eigenvectors, and where the elements of \mathbf{H} and \mathbf{S} are real numbers given by the following integrals extended to the whole space of independent variables, d\mathbf{x}
H_{ik}=\int\varphi_{i}^*\hat{H}\varphi_{k}\,d\mathbf{x}S_{ik}=\int\varphi_{i}^*\varphi_{k}\,d\mathbf{x}Since \mathbf{H} and \mathbf{S} are real and symmetric, all eigenvalues E are real.
S_{il} is called the overlap integral. In the situation where the basis functions (3) are orthonormal, we have:
S_{ik}=\delta_{ik}=\left\{ \begin{array}{ccc}
1 & \implies & i=k\\
0 & \implies & i\neq k
\end{array}\right.where \delta_{ik} is the Kronecker delta. In this case, \mathbf{S} is the identity matrix, \mathbf{S}=\mathbf{I}, and we fall back to the standard eigenvalue problem (1).
Linear algebra dictates that there are two alternatives for system (5) to have a solution: either \det(\mathbf{c})=0 or \det(\mathbf{H}-E\mathbf{S})=0. The first solution is called trivial and is uninteresting, which leads to the following condition:
\begin{equation}\det\left(\mathbf{H}-E\mathbf{S}\right)=0\end{equation}In practice, the Rayleigh-Ritz variational method allows calculating the eigenvalues E without having to calculate the eigenvectors \mathbf{c}.
Determinant (6) leads to a polynomial of degree n, equal to the dimension of the basis (3), and hence to n eigenvalues, which represent an upper bound on the energies of the first n states of the system, the ground state, and the first n-1 excited states.
There is an interesting consideration to make. While the matrices \mathbf{H} and \mathbf{S} are full-ranked—we started from a combination of linearly independent functions, equation (3)—and therefore have non-null determinants (this is a mathematical consequence), the matrix \mathbf{H}-E\mathbf{S} is singular and has a null determinant.
This means that matrix \mathbf{H}-E\mathbf{S} is not full-ranked and the system of linear equations it expresses contains at least one equation linearly dependent on the others, so the choice of coefficients for the eigenvectors is fixed up to a multiplicative factor. System (5) has infinite solutions, all equivalent from a mathematical standpoint.
This is made evident when we substitute each eigenvalue into (5) to obtain the corresponding eigenvector (the coefficients of the wave function \psi in equation (3) for the associated eigenstate). Doing so yields n-1 coefficients as a function of the last one, which can be chosen arbitrarily up to a multiplying factor.
This last coefficient must be fixed by an additional constraint, given by the condition that the probability density is normalized over the whole space, where the probability density is associated, according to the Born rule, to the square modulus of the wave function:
\int \left|\psi\right\|^2\,d\mathbf{x}=\sum_{i=1}^n\sum_{k=1}^n c_i^* c_k\int\varphi_{i}^*\varphi_{k}\,d\mathbf{x}=1C Code
In solving this and other problems numerically, libraries such as GSL and LAPACK/LAPACKE are an invaluable tool.
The following C code calculates eigenvalues and eigenvectors for the secular system we studied. The library used depends on the value of the solver variable in the function godelia_secular_system, which can have one of the values provided by the GODELIA_SOLVER enumerated type. The other arguments to the function use single (for vectors) and double (for matrices) pointers, and their meaning has already been provided in the previous theoretical discussion.
The function returns status = 0 if there are no errors.
#include <gsl/gsl_blas.h>
#include <gsl/gsl_block.h>
#include <gsl/gsl_eigen.h>
#include <gsl/gsl_linalg.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_matrix.h>
#include <gsl/gsl_sf_erf.h>
#include <gsl/gsl_statistics.h>
#include <lapacke.h>
typedef enum {
NO_SOLVER,
GSL,
LAPACK
} GODELIA_SOLVER;
int godelia_secular_system(double **h, double **s, long n, double *e, double **c,
GODELIA_SOLVER solver) {
/* Solves secular system. */
int status = 0, i, j, k, itype, lda, ldb;
char jobz, uplo;
double *h1, *s1, sum;
gsl_matrix *hh, *ss, *eve;
gsl_vector *eva;
gsl_eigen_gensymmv_workspace *w;
switch (solver) {
case NO_SOLVER:
break;
case GSL:
gsl_set_error_handler_off();
hh = gsl_matrix_alloc(n, n);
ss = gsl_matrix_alloc(n, n);
eve = gsl_matrix_alloc(n, n);
eva = gsl_vector_alloc(n);
w = gsl_eigen_gensymmv_alloc(n);
godelia_matrix_to_gsl_matrix(h, hh, n, n);
godelia_matrix_to_gsl_matrix(s, ss, n, n);
godelia_vector_to_gsl_vector(e, eva, n);
godelia_matrix_to_gsl_matrix(c, eve, n, n);
/* Eigensystem */
status = gsl_eigen_gensymmv(hh, ss, eva, eve, w);
gsl_eigen_gensymmv_sort(eva, eve, GSL_EIGEN_SORT_VAL_ASC);
godelia_gsl_matrix_to_matrix(eve, c);
godelia_gsl_vector_to_vector(eva, e);
/* Free memory */
gsl_matrix_free(hh);
gsl_matrix_free(ss);
gsl_matrix_free(eve);
gsl_vector_free(eva);
gsl_eigen_gensymmv_free(w);
break;
case LAPACK:
/* A matrix is replaced by eigenvectors. It must be necessary to
make a copy before the function call. A and B matrices are a
1-dimension arrays. 2D arrays must be tranformed as 1D. If
LAPACK_ROW_MAJOR is defined, row elements are consecutive,
for LAPACK_COL_MAJOR col elements are consecutive. The first
requires a transposition respect to LAPACK_COL_MAJOR and is
thus slower. */
itype = 1; /* This sets the type of generalized eigenvalue problem
that we are solving. We have the possible values
1: Ax = lBx
2: ABx = lx
3: BAx = lx */
jobz = 'V'; /* V/N indicates that eigenvectors should/should not
be calculated. */
uplo = 'U'; /* U/L indicated that the upper/lower triangle of the
symmetric matrix is stored. */
lda = n; // The leading dimension of the matrix A
ldb = n; // The leading dimension of the matrix B
/* Dimensioning h1 and s1 vectors */
h1 = dvector(n * n);
s1 = dvector(n * n);
/* Transforms 2D h and s matrices in a 1D h1 and s1 vectors */
for (k = 0, i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
h1[k] = h[j][i];
s1[k++] = s[j][i];
}
}
/* Solves the generalized eigenvalue problem. Eigenvectors are
* returned in the h1 vector */
status = LAPACKE_dsygv(LAPACK_COL_MAJOR, itype, jobz, uplo, n, h1, lda, s1, ldb,
e);
/* Transforms eigenvectors stored in h1 vector into the 2D c
* matrix */
for (k = 0, i = 0; i < n; i++) {
for (sum = 0, j = 0; j < n; j++) {
c[j][i] = h1[k++];
sum += c[j][i] * c[j][i];
}
/* The computed eigenvectors are normalized to have unit
* magnitude, as done by GSL routine. Unit magnitude
* refers to euclidean distance. */
/* Source: https://math.stackexchange.com/questions/3783729/normalising-eigenvector-to-length-1 */
for (j = 0; j < n; j++)
c[j][i] /= sqrt(sum);
}
/* Freeing memory */
free(h1);
free(s1);
break;
}
return status;
}
GSL is a library that exposes a very well-crafted high-level interface. However, using its calculation functions often requires preparing and dimensioning some objects, as we can see in the previous code. I never remember the correct sequence, which also depends on which function we’re using.
The following functions are my way of simplifying code when using GSL and allow me to transform C pointers into arrays usable by GSL and vice versa. Thus, the godelia_secular_system wrapper function returns C pointers consistent with the calculation’s needs.
void godelia_matrix_to_gsl_matrix(double **m, gsl_matrix *g, long r, long c) {
/* For double data */
int i, j, k;
/* gsl matrix object store matrixes in a vector (array 1D) */
for (k = 0, i = 0; i < r; i++) {
for (j = 0; j < c; j++) {
g->data[k++] = m[i][j];
}
}
}
void godelia_gsl_matrix_to_matrix(gsl_matrix *m, double **x) {
int i, j, c = 0;
for (i = 0; i < m->size1; i++) {
for (j = 0; j < m->size2; j++) {
x[i][j] = m->data[c++];
}
}
}
void godelia_vector_to_gsl_vector(double *v, gsl_vector *g, long n) {
/* For double data */
int i;
for (i = 0; i < n; i++) g->data[i] = v[i];
}
void godelia_gsl_vector_to_vector(gsl_vector *v, double *x) {
int i;
for (i = 0; i < v->size; i++) {
x[i] = v->data[i];
}
}
Conclusions
Numerical computation is, in my opinion, one of the most exciting and challenging areas of work for a programmer. Understanding the internals and architecture of the libraries we use requires knowledge of the theory underlying the problem we’re trying to solve.
In practice, the procedure we’ve outlined in this article.






