Francisco Yepes Barrera 
https://unsplash.com/photos/a-close-up-of-a-sheet-of-paper-with-numbers-on-it-5z70PsbFCMM?utm_content=creditShareLink&utm_medium=referral&utm_source=unsplash
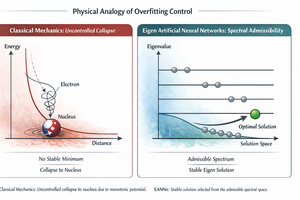
Degeneration occurs when two or more independent wave functions have the same eigenvalue.
It is said that \(n\) functions \( f_ {1}, f_ {2,} \ldots, f_ {n}\) are linearly independent if the condition
$$\sum_{i}c_{i}f_{i}=0$$
It is satisfied when all the constants \(c_ {i}\) are equal to zero.
The degree of degeneration of a system is the number of linearly independent functions with the same eigenvalue.
Theorem. Any linear combination of \(n\) functions of a degenerate level of energy \(E\) is also an eigenfunction of the Hamiltonian with energy \(E\).
The proof is straightforward:
$$\hat{H}\psi_{1}=E\psi_{1},\hat{H}\psi_{2}=E\psi_{2},\ldots,\hat{H}\psi_{n}=E\psi_{n}$$
$$\varphi=\sum_{i}c_{i}\psi_{i}$$
$$\hat{H}\varphi=\hat{H}\sum_{i}c_{i}\psi_{i}=E\sum_{i}c_{i}\psi_{i}$$
$$\hat{H}\sum_{i}c_{i}\psi_{i}=\sum_{i}c_{i}\hat{H}\psi_{i}=\sum_{i}c_{i}E\psi_{i}=E\sum_{i}c_{i}\psi_{i}=E\varphi$$
